먼저 이번 내용은 회귀선의 정도의 글에서의 연장선의 내용으로
회귀선의 정도를 측정하는 데 있어서
- 추정값의 표준오차
- 결정계수
2가지 경우에 대해서 알아보았었습니다.
이번에는 상관분석에서의 상관계수와
분산분석에서의 F-검정으로부터 측정하는 내용에 대해서 다루어 보려고 합니다
상관분석
상관계수
두 변수 x와 y 사이의 상관관계를 설명하는 데 결정계수가 쓰이기도 하지만,
결정계수는 x와 y의 관계가 음의 상관관계인지 양의 상관관계인지를 구별하지 못하는 단점을 가지고 있습니다.
이와 같은 단점을 보완하여 두 변량 간의 상호관계를 측정하는 측도로서 상관관계가 있습니다.
상관관계 r을 다음과 같이 구할 수 있습니다.
$$ r = \pm \sqrt {r^2} $$
즉, 결정계수 r ² 의 제곱근이며,
만약 추정된 회귀선의 기울기 b₁ 이 양이면 양의 상관계수를 갖고
$$r = \sqrt {r^2}$$ 기울기 b₁ 이 음이면 음의 상관계수를 가집니다.
$$r = - \sqrt {r^2}$$
결정계수 r ² 의 값이 0에서 1까지이므로 상관계수 r의 값은 -1에서 1까지이며
x와 y의 상관정도에 따라서 r의 값이 결정됩니다.
단순회귀분석에서는 x와 y의 함수관계를
$$ y = \beta_0 + \beta_1x + \epsilon$$
이와 같은 회귀모형식으로 나타내고
이때 y 만 확률 변수이고 x는 확률변수가 아니었는데(수학변수)
만약 x 도 또한 확률변수이고 x와 y 가 어떤 이변량분포를 하고 있다면
x와 y의 모집단상관계수는 다음과 같이 정의합니다.
$$ \rho_{xy} = \frac{Cov(x,y)}{\sqrt{Var(x)Var(y)}} = \frac{\sigma_{xy}}{\sigma_x \sigma_{y}} $$
모집단으로부터 크기가 n인 표본을 뽑았을 때 n개의 자료점이 얻어졌다면 이 두 변수 사이의 표본상관계수는
$$ r_{xy} = \frac{S_{(xy)}}{\sqrt{S_{(xx)} S_{(yy)}}} $$
다음과 같이 정의됩니다.
이때 상관계수는 두 변수 간의 선형관계가 어느 정도인가를 재는 측도이지
함수관계를 알아보는 측도는 아닙니다. (두 변수 간의 직선적인 관련성만을 측정하는 도구)
아래의 그림은 상관계수 값에 대한 예시로 상관계수에 대한 이해를 돕고자 가지고 왔습니다.
[출처] https://otexts.com/fppkr/graphics-scatterplots.html

이후 알아보게 될 중회귀나 곡선회귀에서 얻어지는 결정계수로부터는
상관계수 r을 구할 수 없기 때문에 상관계수 r을 구할 때에는
결정계수 r ² 의 값이 반드시 단순회귀분석에서 얻어지는 결정계수인가를 확인하여야 합니다.
분산분석
주어진 자료를 적합시키는 데 있어서 회귀직선이 유의한가 하는 것은 SSR이 상대적으로 SSE보다 어느 정도 큰가를 분산분석표를 만들어 알아볼 수 있습니다
이때 이전의 내용을 다시 가져와보면 SSR과 SSE의 의미는 다음과 같습니다.
SST : 총 변동 (전체제곱합)
SSE : 회귀선에 의해서 설명 안 되는 변동 (잔차제곱합)
SSR : 회귀선에 의하여 설명되는 변동 (회귀제곱합)
분산분석표를 보면 다음과 같습니다.
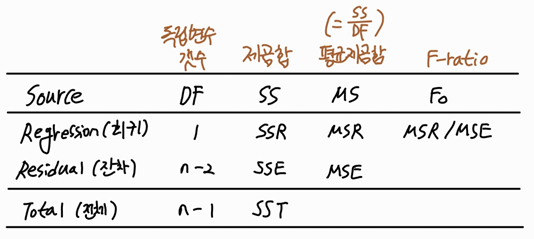
위의 분산분석표에서 MSE(Mean Squared Error) 에 대해서 보면
$$ MSE = \frac{SSE}{n-2} $$이 부분에 대해 추정값의 표준오차를 구하는 과정에서의
회귀로부터의 평균제곱편차를 다음과 같이 정의했었는데
$$ {s_{y|x}}^2=\frac{\sum e_i^2}{n-2}=\frac{\sum (y_i-\hat y_i)^2}{n-2} $$
다시 표현하면 다음과 같이 나타낼수 있다
$$ {s_{y|x}}^2=\frac{\sum e_i^2}{n-2}=\frac{\sum (y_i-\hat y_i)^2}{n-2} = \frac{SSE}{n-2} = MSE $$
다음으로 F₀ (F-ratio)보면
F₀ (F-ratio)는 회귀의 평균제곱 MSR과 잔차의 평균제곱 MSE 와의 비율입니다.
$$ F_{0}=\frac{MSR}{MSE} $$
이 비율이 크면 회귀제곱합이 잔차제곱합보다 상대적으로 커서 회귀선이 x와 y 간의 관계를 설명하는 데 유의하다는 의미가 됩니다.
가설검정의 내용을 추가하여 학습해 보면
가설이 다음과 같을 때
$$ H_0:\beta_1=0$$$$H_a:\beta_1\neq 0 $$
이와 같은 식이 성립한다면
$$ F_{0}> F_\alpha(1,n-2) $$
귀무가설을 기각해서 β₁ ≠ 0라고 할 수 있고
회귀선이 유의하다고 말합니다.
예제를 통한 회귀선의 정도 측정
예제를 통해 추정된 회귀선의 정도를 측정하는 방법을 적용시켜 보겠습니다.
예시로 부동산 자료의 회귀분석에 대한 SAS output을 이용하면
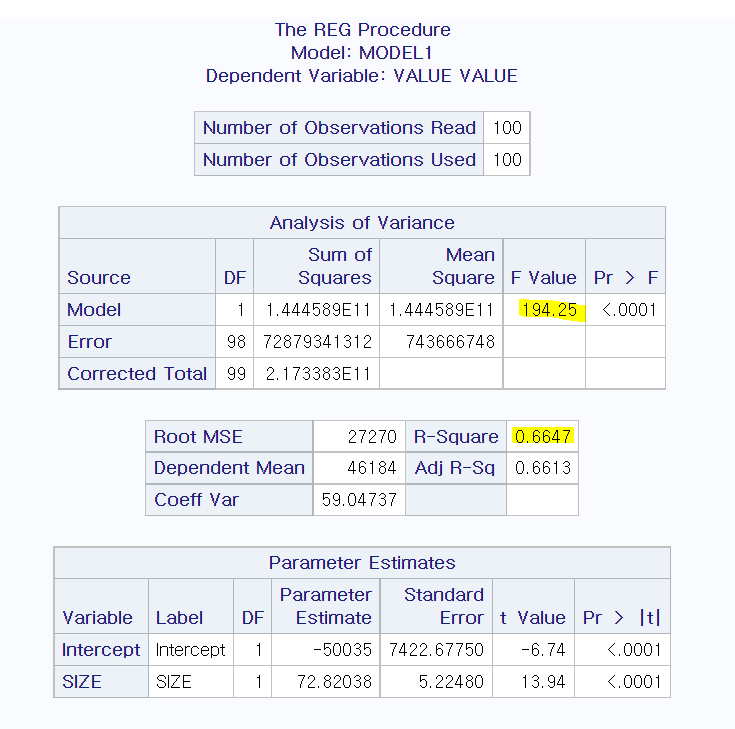
① R² (결정계수)를 이용
R² = 0.6647 or 66.47%
=> 회귀선이 자료의 66.47% 설명한다,
② F₀ 이용
가설이 다음과 같을 때
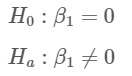
F₀ = 194.25이고
F분포표를 통해
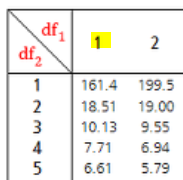
***
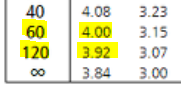
유의 수준 5%에서
F₀.₀₅(1, 98)의 값은 약 (4.00+3.92)/2=3.96
194.25 > 3.96 임으로 귀무가설을 기각할 수 있다.
따라서 β₁ ≠ 0
즉 "size(x)와 value(y) 간에 유의미한 관계이다."라고 할 수 있다.
정리하면
회귀선의 정도를 측정하는 데 있어
상관분석과 분산분석에 대해서 배움으로써
- 추정값의 표준오차
- 결정계수
- 상관계수
- F₀ (F-ratio)
기존내용에서 추가적으로 2가지에 대해서 더 알아보았습니다.
'통계 > 회귀분석' 카테고리의 다른 글
| [단순회귀분석] 단순회귀에 관한 추론 (0) | 2024.01.10 |
|---|---|
| [단순회귀분석] 회귀선의 정도 (1) | 2024.01.05 |
| [단순회귀분석] 회귀선의 추정 (2) | 2024.01.04 |
| [단순회귀분석] 회귀분석의 기본개념 (0) | 2024.01.04 |
| [머리말] 회귀분석이란 (0) | 2024.01.03 |