표본자료로부터 선형식을 추정하여 얻은 직선은 다음과 같습니다.
$$y = b_0 + b_1x$$
이와 같은 직선을 추정된 회귀직선, 또는 간단히 회귀선이라고 합니다.
이때 b₀, b₁ 는 각각 β₀, β₁ 의 추정값으로 b₀는 절편, b₁는 기울기에 해당합니다.
이번 글에서는 b₀, b₁ 를 구하는 방법을 소개하려고 합니다.
최소제곱법
최소제곱법(Least Square Method)이란 오차를 최소화하여 회귀계수인 β₀, β₁를 추정하는 기법을 말합니다.
최소제곱법을 이용하여 최소제곱추정량(Least Squares Estimators)을 구하면 β₀, β₁의 추정량을 구할 수 있습니다.
$$ y_i = \beta_0 + \beta_1x_i + \epsilon_i$$
이와 같이 가정하고 이 식을 회귀모형식(Regression Model Equation)이라고 합니다.
추정된 회귀선(Estimated Regression Line)은 다음과 같습니다.
$$\hat y_i = \hat \beta_0 + \hat \beta_1x_i = b_0 + b_1x_i$$
이 식을 회귀모형식에 대입하여 전개를 하면 (오차제곱합을 Q라고 하자)
$$minimize\; Q = \sum_{i=1}^{n}\epsilon_i^{2} = \sum_{i=1}^{n}(y_i - \widehat{y_i})^{2} = \sum_{i=1}^{n}(y_i - b_0 - b_1x_i)^{2}$$
Q(오차제곱합)의 최소값을 구하려면 기울기가 0이 되는 값을 찾으면 됨으로
$$\frac{\partial Q}{\partial b_0} = 2\sum_{i=1}^{n}(y_i-b_0-b_1x_i)\cdot (-1) = 0$$
$$\frac{\partial Q}{\partial b_1} = 2\sum_{i=1}^{n}(y_i - b_0 - b_1x_i)\cdot (-x_i) = 0$$
두 식을 전개하면
$$\sum_{i=1}^{n}y_i - b_0n -b_1\sum_{i=1}^{n}x_i = 0$$
$$\sum_{i=1}^{n}x_iy_i - b_0\sum_{i=1}^{n}x_i -b_1\sum_{i=1}^{n}x_i^2 = 0$$
정리하면
$$\sum_{i=1}^{n}y_i = b_0 n + b_1\sum_{i=1}^{n}x_i $$
$$\sum_{i=1}^{n}x_iy_i = b_0 \sum_{i=1}^{n} x_i + b_1 \sum_{i=1}^{n} x_i^2 $$
이 식을 정규방정식이라고 합니다.
다음으로 위의 식에서 b₀ 와 b₁을 구하면
$$b_0 = \overline{y} - b_1\overline{x}$$
$$b_1 = \frac{\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i=1}^{n}(x_i-\overline{x})^2}\overset{\underset{\mathrm{let}}{}}{=}\frac{S_{xy}}{S_{xx}}$$
이와 같은 방법으로 얻어진 β₀, β₁의 추정량을 최소제곱추정량이라고 합니다.
이때 표현의 편의를 위해 다음과 같이 나타낸다.
$$ S_{xx} = \sum_{i=1}^{n}(x_i-\overline{x})^2 = \sum x_i^2 - \frac{(\sum x_i)^2}{n}$$$$ S_{yy} = \sum_{i=1}^{n}(y_i-\overline{y})^2= \sum y_i^2 - \frac{(\sum y_i)^2}{n}$$$$ S_{xy} = \sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y}) = \sum x_i y_i -\frac{\sum x_i \sum y_i}{n}$$
위의 내용을 정리하면 다음과 같습니다.
절편의 추정량(β₀의 추정량)
$$b_0 = \hat \beta_0=\overline{y}-b_1\overline{x}$$
기울기 추정량(β₁의 추정량)
$$b_1 = \hat \beta_1=\frac{S_{xy}}{S_{xx}}$$
따라서 b₀ 와 b₁값을 알 수 있기 때문에 추정된 회귀선을 구할 수 있게 됩니다.
다음으로 예시를 통해 위의 개념을 적용해 보겠습니다.
자료가 다음과 같이 주어졌을 때
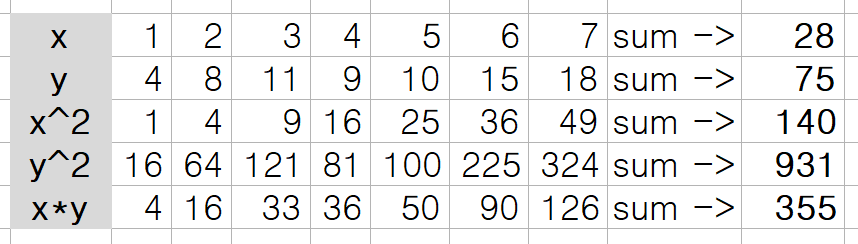
$$b_1 = \frac{\sum_{i=1}^{n}x_iy_i-\frac{1}{n}\sum_{i=1}^{n}x_i\sum_{i=1}^{n}y_i}{\sum_{i=1}^{n}x_i^2-\frac{1}{n}(\sum_{i=1}^{n}x_i)^2}=\frac{335-\frac{1}{7}(28)(75)}{140-\frac{1}{7}(28)^2}=1.25$$
$$b_0 = \overline{y} - b_1\overline{x}=5.714$$
따라서 추정된 회귀선은 다음과 같습니다.
$$\widehat{y}=5.714+1.25x$$
최대가능도추정법
최소제곱법에 의하여 회귀계수인 β₀, β₁를 추정하는 방법은 오차항 ε가 정규분포를 한다는 가정이 없을 때에도 적용되는 추정량법입니다.
이제 오차항 ε 가 정규분포를 하는 확률변수로서 0을 평균으로 하고 σ² 을 분산으로 하는 성질을 가진다고 가정합니다.
$$\epsilon \sim{} N(0,\sigma^{2})$$
εᵢ 의 확률밀도함수는
$$ f(\epsilon_i) = \frac{1}{\sqrt{2\pi\sigma^2}}exp(-\frac{\epsilon_i^2}{2\sigma^2}) $$
f(εᵢ) , i = 1,2,...,n 들의 곱은$$ L =\prod_{i=1}^{n}f(\epsilon_i)= \frac{1}{(2\pi \sigma ^2)^{n/2}} exp[-\frac{\sum \epsilon_i^2}{2 \sigma ^2}] = \frac{1}{(2\pi \sigma ^2)^{n/2}} exp[-\frac{\sum (y_i - \beta_0-\beta_1x_i)^2}{2 \sigma ^2}] $$
이 함수는 가능도함수(likelihood function)이고 이 함수를 최대로 크게 하는 β₀ 와 β₁ 의 추정량을 최대가능도추정량 (maximum likelihood estimator)입니다.
가능도함수에 로그를 취한 로그가능도함수(log-likelihood function)는 다음과 같습니다.
$$ ln L = -\frac{n}{2}ln2\pi\sigma^2-\frac{1}{2\sigma^2}\sum(y_i-\beta_0-\beta_1x_i)^2 $$
각각 β₀, β₁ 으로 편미분 하면
$$ \frac{\partial ln L}{\partial \beta_0} = \frac{1}{\sigma^2}\sum(y_i-\beta_0-\beta_1x_i) $$
$$ \frac{\partial ln L}{\partial \beta_1} = \frac{1}{\sigma^2}\sum x_i(y_i-\beta_0-\beta_1x_i) $$
이후로는 각각 0으로 놓고 푸는 것과 동일하고 이 내용은 최대가능도추정량의 b₀ 와 b₁ 은 최소제곱추정량과 동일함을 알 수 있습니다
이때 최대가능도추정량과 최소제곱추정량과의 차이는 최대가능도추정량은 오차항 εᵢ 의 분포를 정규분포 N(0, σ² )이라고 가정하고 얻어지는 값이고, 최소제곱추정량은 이러한 가정이 전제되어있지 않다는 점입니다.
적합된 회귀선의 성질
추정된 회귀선은 다음과 같은데
$$\hat y_i = \hat \beta_0 + \hat \beta_1x_i = b_0 + b_1x_i$$
여기서 xᵢ 에서 관찰된 yᵢ와 추정된 ŷ ᵢ 과의 차이는 다음과 같고
$$ e_i = y_i - \hat y_i $$
이를 잔차라고 합니다.
b₀ 와 b₁ 의 값이 최소제곱법을 통해 구해진 최소제곱추정값이면 다음의 성질을 성립합니다
(1) 잔차들의 합은 0이다.
$$ \sum e_i = 0 $$
이 성질은 다음과 같이 증명할 수 있습니다.
$$ \sum e_i = \sum (y_i - \hat y_i ) = \sum (y_i - b_0 - b_1 x_i) = \sum y_i - n b_0 - b_1 \sum x_i $$
이때의 이 부분의 식은
$$ \sum y_i - n b_0 - b_1 \sum x_i $$
정규방정식을 이용하여 증명을 하면
$$\sum_{i=1}^{n}y_i - b_0n -b_1\sum_{i=1}^{n}x_i = 0$$
$$\sum_{i=1}^{n}x_iy_i - b_0\sum_{i=1}^{n}x_i -b_1\sum_{i=1}^{n}x_i^2 = 0$$
정규방정식의 첫 번째 식에 의해
$$ \sum e_i = \sum y_i - n b_0 - b_1 \sum x_i = 0 $$
이와 같이 증명이 됩니다.
(2) 잔차들의 xᵢ 에 의한 가중합은 0이다.
$$ \sum x_i e_i = 0 $$
이 성질은 다음과 같이 증명할 수 있습니다.
식을 먼저 전개하면 다음과 같고
$$ \sum x_i e_i = \sum x_i (y_i - \hat y_i ) = \sum x_i (y_i - b_0 - b_1 x_i) = \sum x_i y_i - b_0 \sum x_i - b_1 \sum x_i ^2 $$
정규방정식을 이용하여 증명을 하면
$$\sum_{i=1}^{n}y_i - b_0n -b_1\sum_{i=1}^{n}x_i = 0$$
$$\sum_{i=1}^{n}x_iy_i - b_0\sum_{i=1}^{n}x_i -b_1\sum_{i=1}^{n}x_i^2 = 0$$
정규방정식의 두 번째 식에 의해
$$ \sum x_i e_i = \sum x_i y_i - b_0 \sum x_i - b_1 \sum x_i ^2 = 0 $$
이와 같이 증명이 됩니다.
(3) 잔차들의 ŷ에 의한 가중합은 0이다.
$$ \sum \hat y_i e_i = 0 $$
이 성질은 다음과 같이 증명할 수 있습니다.
$$ \sum \hat y_i e_i = \sum ( b_o + b_1 x_i ) e_i = b_0 \sum e_i + b_1 \sum x_i e_i $$
이때 위 2가지 성질에 의해서
$$ \sum e_i = 0 $$$$ \sum x_i e_i = 0 $$
위의 성질을 이용하면
$$ \sum \hat y_i e_i = b_0 \sum e_i + b_1 \sum x_i e_i =0 $$
이와 같이 증명이 됩니다.
따라서 다음의 성질을 만족하게 됩니다.
(1) 잔차들의 합은 0이다. $$\sum e_i = 0 $$
(2) 잔차들의 xᵢ 에 의한 가중합은 0이다. $$ \sum x_i e_i = 0 $$
(3) 잔차들의 ŷ에 의한 가중합은 0이다. $$ \sum \hat y_i e_i = 0 $$
정리하면
- 최소제곱법
오차를 최소화하여 회귀계수인 β₀, β₁를 추정하는 기법
최소제곱법을 이용하여 최소제곱추정량을 구하면 β₀, β₁의 추정량인 b₀ 와 b₁값을 구할 수 있다.
- 최대가능도추정법
최대가능도추정량은 오차항 εᵢ 의 분포를 정규분포 N(0, σ²)이라고 가정하고 얻어지는 값
- 적합된 회귀선의 성질
성질 ① : 잔차들의 합은 0이다.
성질 ② : 잔차들의 xᵢ 에 의한 가중합은 0이다.
성질 ③ : 잔차들의 ŷ에 의한 가중합은 0이다.
'통계 > 회귀분석' 카테고리의 다른 글
| [단순회귀분석] 단순회귀에 관한 추론 (0) | 2024.01.10 |
|---|---|
| [단순회귀분석] 상관분석과 분산분석 (0) | 2024.01.05 |
| [단순회귀분석] 회귀선의 정도 (1) | 2024.01.05 |
| [단순회귀분석] 회귀분석의 기본개념 (0) | 2024.01.04 |
| [머리말] 회귀분석이란 (0) | 2024.01.03 |