구간에 대한 추정을
y에 대한 평균인 조건부기댓값에 대한 예측과
y의 각각의 값에 대한 예측으로 나누어질수 있는데
각각의 경우에 대해서 알아보자
조건부 기댓값에서의 추정
구간에 대한 추정을 구하기 위해서 표준편차가 필요하다.
이전 "단순회귀분석에서의 추론"라는 글에서 조건부기댓값의 분포를 구했었는데
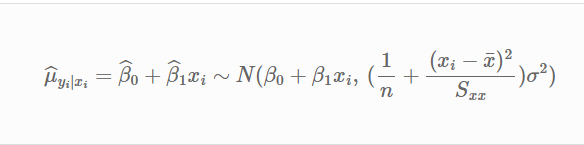
이러한 분포에서의 표준편차를 다시 써보면
$$S_m=S_e\sqrt{\frac{1}{n}+\frac{(x_m-\bar{x})^2}{(n-1)S_x^2}}$$
(이때 Sₘ은 평균에 대한 표준편차(Standard Error of the Mean))
다른 형태로 다음과 같이 표현도 가능하다.
$$S_m=\sqrt{MSE(\frac{1}{n}+\frac{(x_m-\bar{x})^2}{S_{xx}})}$$
조건부 기댓값의 구간에 대한 추정을
$$\hat{y}_m \pm t_{\alpha/2}(n-2)\times S.E.(\hat{y}_m)$$
다음과 같은 신뢰구간(Confidence Interval)(CI)을 이용하여 구하면
$$\hat{y}_m \pm t_{\alpha/2}(n-2)\times \sqrt{MSE(\frac{1}{n}+\frac{(x_m-\bar{x})^2}{S_{xx}})}$$
다음과 같은 자료를 통해 보면

x=50인 지점에서의 신뢰구간은 다음과 같이 나타난다.
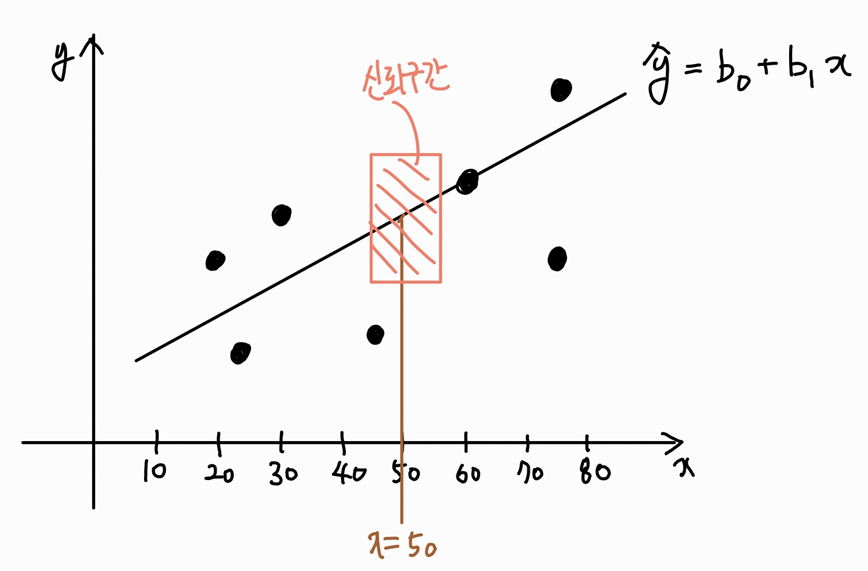
신뢰구간을 구하기 위해 먼저 표준편차를 구하면
$$S.E.(\hat{y}_m)=\sqrt{MSE(\frac{1}{n}+\frac{(50-\bar{x})^2}{S_{xx}})}$$
이러한 값을 이용해 신뢰구간은 다음과 같이 나온다.
$$\hat{y}_m \pm t_{\alpha/2}(n-2)\times \sqrt{MSE(\frac{1}{n}+\frac{(50-\bar{x})^2}{S_{xx}})}$$
y의 각각의 값에서의 구간에 대한 추정
예측표준오차(Prediction Standard Error)를 Sₚ라 하고
오차의 표준편차를 Sₑ라고 할때
수식으로 다음과 관계가 있다.
$$S_p^2=S_m^2+S_e^2 $$
이런 관계를 통해 예측표준오차는
다음과 같이 나타낼수 있다.
$$S_p=S_e\sqrt{1+\frac{1}{n}+\frac{(x_m-\bar{x})^2}{(n-1)S_x^2}}$$
다른 형태로 다음과 같이 표현도 가능하다.
$$S_p=\sqrt{MSE(1+\frac{1}{n}+\frac{(x_m-\bar{x})^2}{S_{xx}})}$$
y의 각각의 값에서의 구간을 예측구간(prediction interval)(PI)라고 하고
예측구간을 수식으로 표현하면
$$\hat{y}_m \pm t_{\alpha/2}(n-2)\times S_p(\hat{y}_m)$$
정리하면
$$\hat{y}_m \pm t_{\alpha/2}(n-2)\times \sqrt{MSE(1+\frac{1}{n}+\frac{(x_m-\bar{x})^2}{S_{xx}})})$$
그림을 통해 신뢰구간과 예측구간을 비교해보면
다음과 같이 나타낼 수 있다.

SAS코드를 이용한 예시
이전에 사용했던 부동산 자료를 이용해
SAS에서의 신뢰구간과 예측구간을 구하는 예시를 보이면
x(변수 value)가 10000인 지점에서의 신뢰구간과 예측구간을 구한다고 했을때
SAS코드를 다음과 같이 입력하여

결과값을 보면

***

x = 10000일때
신뢰구간(CI)는 914.35 to 1067.74
예측구간(PI)는 380.33 to 1601.75
이와 같이 나타남을 알 수 있다.
'통계 > 통계의 첫 한입 물었을 시기' 카테고리의 다른 글
| 중회귀분석에서의 추론 (0) | 2023.02.02 |
|---|---|
| 중회귀분석 (0) | 2023.01.28 |
| 회귀적합도 (0) | 2023.01.15 |
| 단순회귀분석에서의 검정 (0) | 2023.01.13 |
| 단순회귀분석에서의 추론 (0) | 2023.01.10 |